Fast Polynomial Evaluation for Correctly Rounded Elementary Functions using the RLIBM Approach

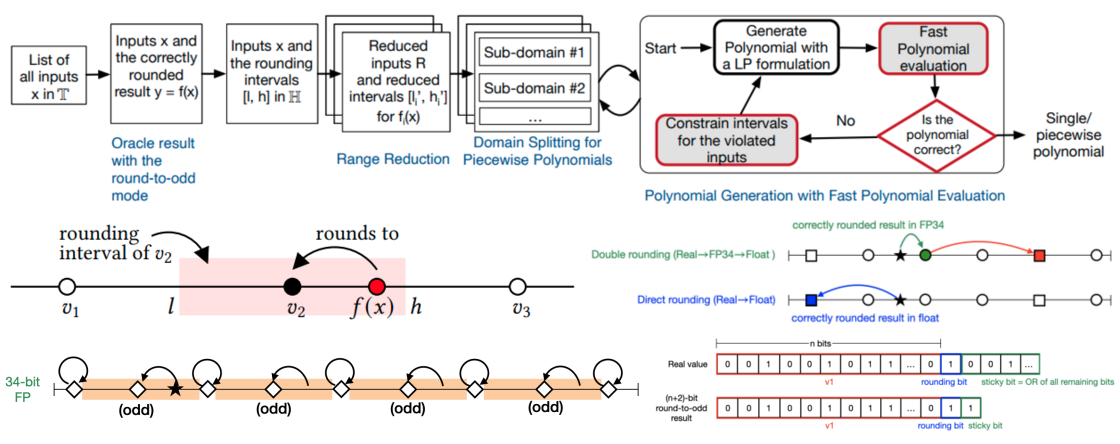
Abstract: This paper proposes fast polynomial evaluation methods for correctly rounded elementary functions generated using our Rlibm approach. The resulting functions produce correct results for all inputs with multiple representations and rounding modes. Given an oracle, the Rlibm approach approximates the correctly rounded result rather than the real value of an elementary function. A key observation is that there is an interval of real values around the correctly rounded result such that any real value in it rounds to the correct result. This interval is the maximum freedom available to Rlibm's polynomial generation procedure. Subsequently, the problem of generating correctly rounded elementary functions using these intervals can be structured as a linear programming problem. Our prior work on the Rlibm approach uses Horner's method for polynomial evaluation. This paper explores polynomial evaluation techniques such as Knuth's coefficient adaptation procedure, parallel execution of operations using Estrin's procedure, and the use of fused multiply-add operations in the context of the Rlibm approach. If we take the polynomial generated by the Rlibm approach and subsequently perform polynomial evaluation optimizations, it results in incorrect results due to rounding errors during polynomial evaluation. Hence, we propose to integrate the fast polynomial evaluation procedure in the Rlibm's polynomial generation process. Our new polynomial evaluation procedure that combines parallel execution with fused multiply-add operations outperforms the Horner's method used by Rlibm's correctly rounded functions. We show the resulting polynomials for 32-bit float are not only correct but also faster than prior functions in Rlibm by 24%.