5.1. Newton’s Method

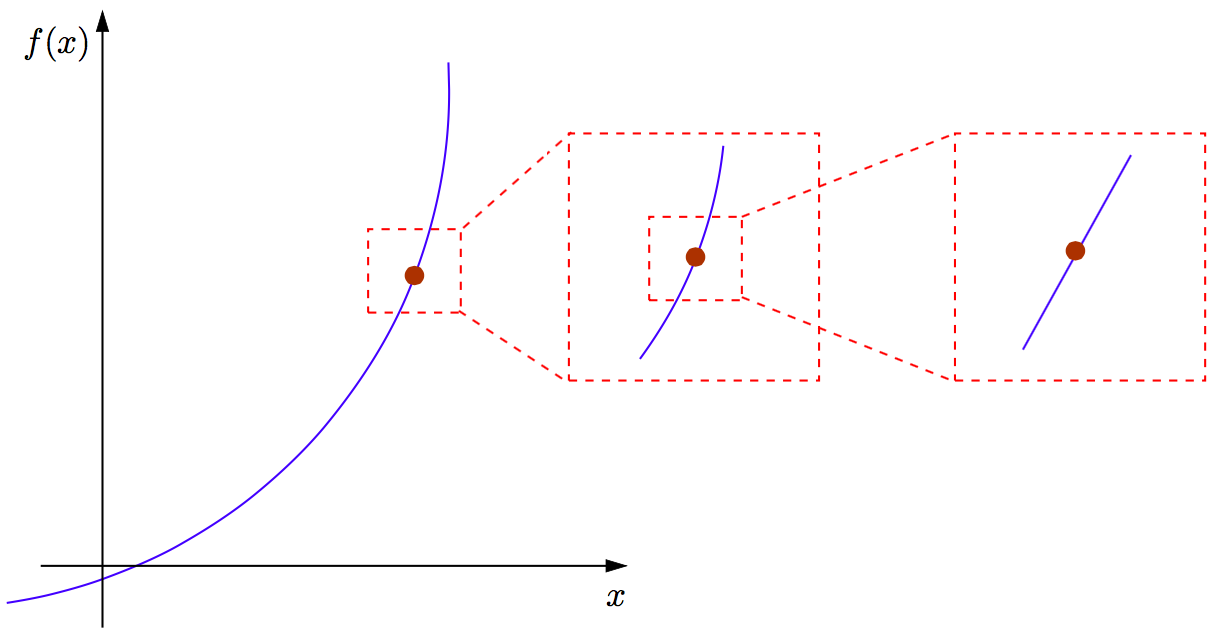
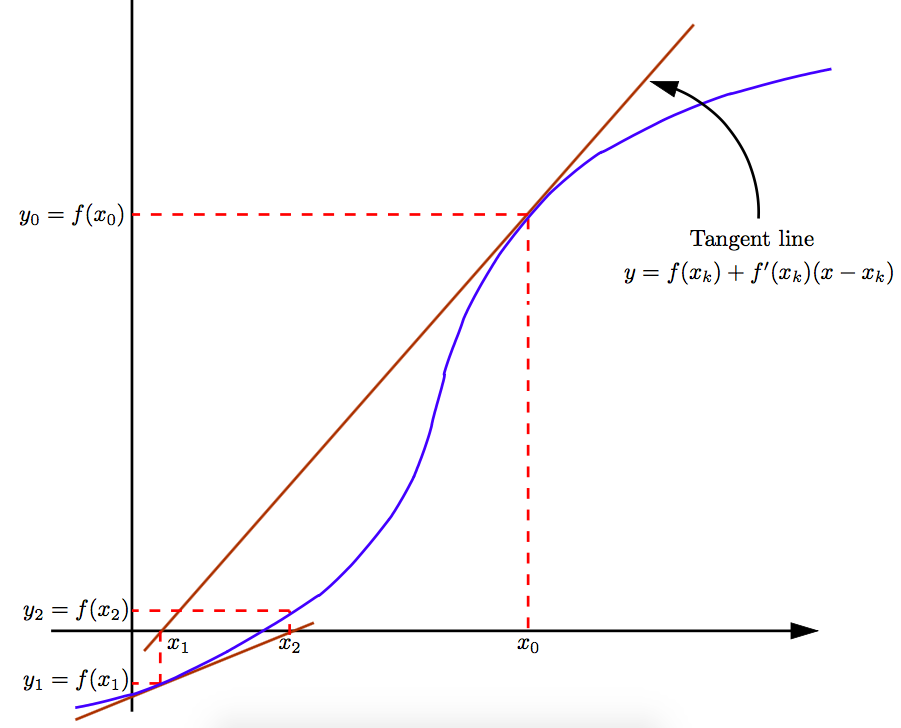
This example is a special case of an algorithm for solving nonlinear equations known as Newton’s method (also called the Newton-Raphson method). The general idea is as follows: if we “zoom” close enough to any smooth function, its graph looks more and more like a straight line (specifically, the tangent line to the curve). Newton’s method suggests: if after \(k\) iterations we have approximated the solution of \(f(x)=0\) (a general nonlinear equation) as \(x_k\), then:

_images/newton.png
  • Form the tangent line at \((x_k,f(x_k))\).
  • Select \(x_{k+1}\) as the intersection of the tangent line with the horizontal axis (\(y=0\)).

If \((x_n,y_n)=(x_n,f(x_n))\), the tangent line to the plot of \(f(x)\) at \((x_n,y_n)\) is:

\[y-y_n=\lambda(x-x_n), \enspace\enspace \mbox{where $\lambda=f'(x_n)$ is the slope}\]

Thus, the tangent line has equation \(y-y_n=f'(x_n)(x-x_n)\).

_images/newton-iteration.png

Setting \(y=0\) gives

\[-f(x_n)=f'(x_n)(x-x_n)\Rightarrow x=x_n-\frac{f(x_n)}{f'(x_n)}=x_{n+1}\]

Ultimately, Newton’s method reduces to:

(1)\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\]

Our previous example (square root of \(a\)) is just an application of Newton’s method to the nonlinear equation \(f(x)=x^2-a=0\). Applying equation (1) gives:

\[x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)}=x_k-\frac{x_k^2-a}{2x_k}=\frac{2x_k^2-x_k^2+a}{2x_k}=\frac{x_k^2+a}{2x_k}\]

which is the same iteration we considered previously. A few comments about Newton’s method:

  • It requires the function \(f(x)\) to be not only continuous, but differentiable as well. We will later see variants that do not explicitly require knowledge of \(f'\). This would be an important consideration if the formula for \(f'(x)\) is significantly more complex and expensive to evaluate than \(f(x)\), or if we simply do not possess an analytic expression for \(f'\) (this could be the case if \(f(x)\) is not given to us via an explicit formula, but only defined via a black-box computer function that computes the value).

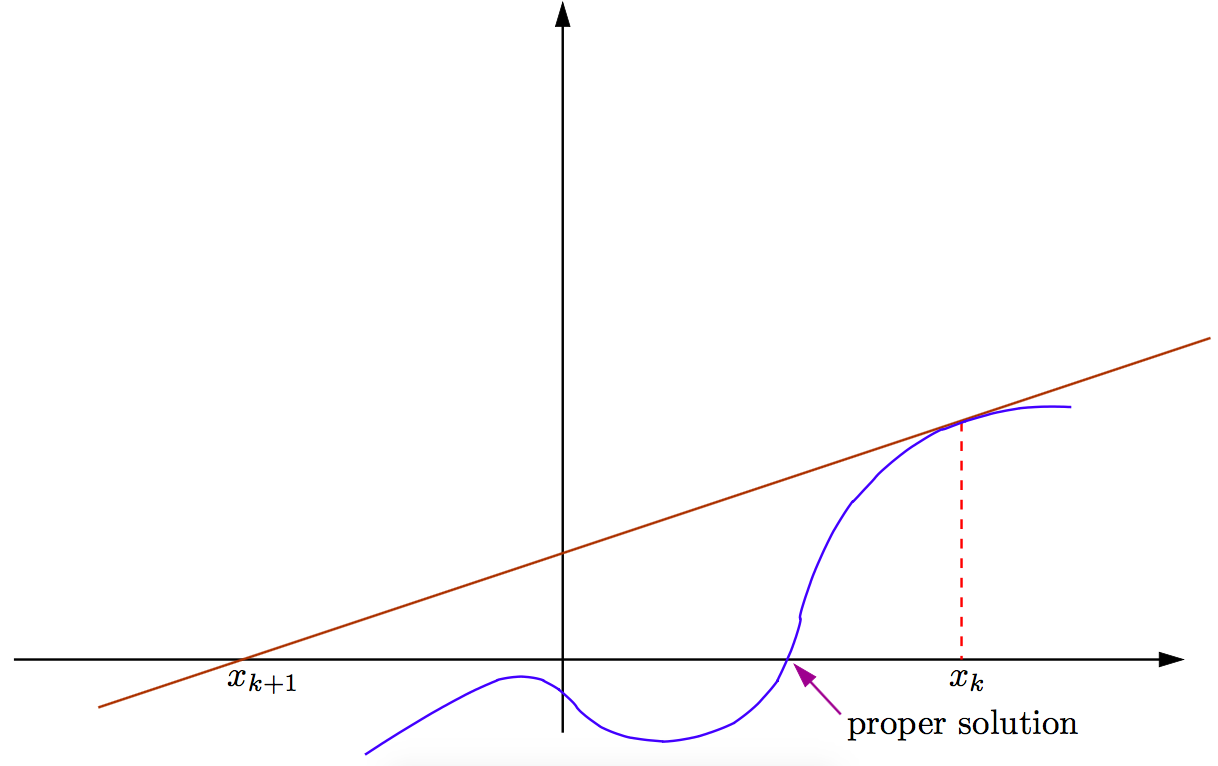
  • If we ever have an approximation \(x_k\) with \(f'(x_k)\approx 0\), we should expect problems, especially if we are not close to a solution (we would be nearly dividing by zero). In such cases, the tangent line is almost (or exactly) horizontal. Thus, the next iterate can be a very remote value and convergence may be far from guaranteed.

    _images/newton-convergence.png