5.5. The Bisection Method

Newton’s method is a popular technique for the solution of nonlinear equations, but alternative methods exist which may be preferable in certain situations. The Bisection method is yet another technique for finding a solution to the nonlinear equation \(f(x)=0\), which can be used provided that the function \(f\) is continuous. The motivation for this technique is drawn from Bolzano’s theorem for continuous functions:

Theorem (Bolzano)

If the function \(f(x)\) is continuous in \([a,b]\) and \(f(a)f(b)<0\) (i.e., the function has values with different signs at \(a\) and \(b\)), then a value \(c\in (a,b)\) exists such that \(f(c)=0\).

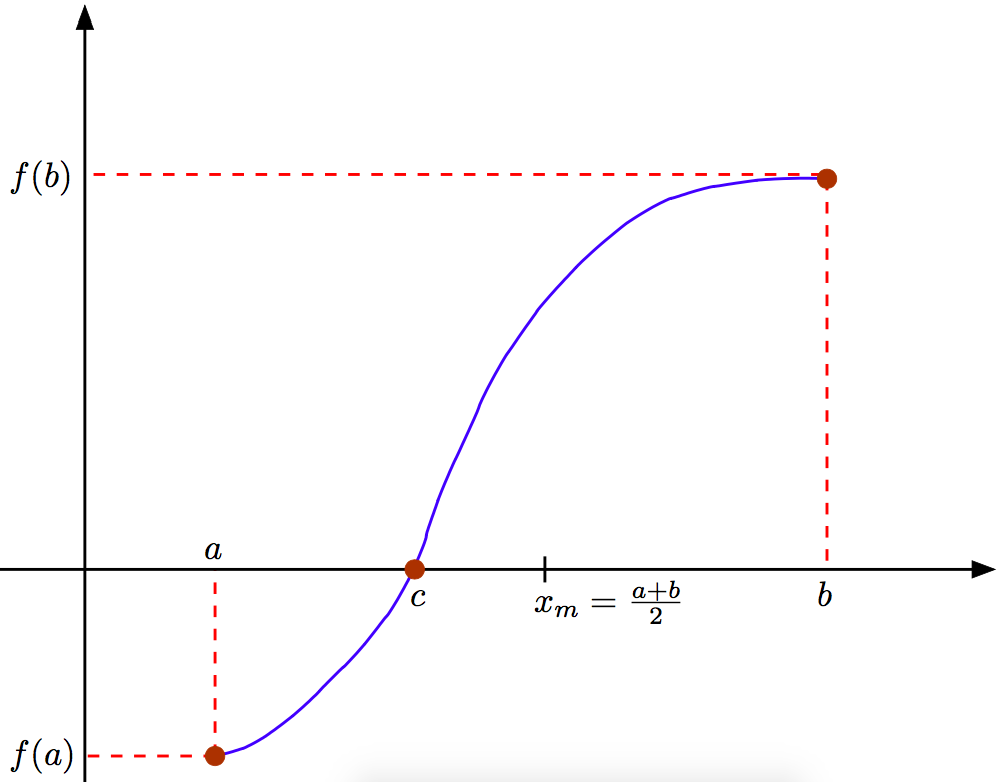
The bisection algorithm attempts to locate the value \(c\) where the graph of \(f\) crosses over zero, by checking whether it belongs to either of the two sub-intervals \([a,x_m]\), \([x_m,b]\), where \(x_m\) is the midpoint

\[x_m=\frac{a+b}{2}\]

The algorithm proceeds as follows:

• If \(f(x_m)=0\), we have our solution \((x_m)\) and the algorithm terminates.

• In the much more likely case that \(f(x_m)\neq 0\), we observe that \(f(x_m)\) must have the opposite sign than one of \(f(a)\) or \(f(b)\) (since they have opposite signs themselves). Thus,

  • Either \(f(a)f(x_m)<0\), or
  • \(f(x_m)f(b)<0\).

  We pick whichever of these two intervals satisfies the condition, and continue the bisection process with it.

Convergence: Let us conventionally define the “approximation” at \(x_k\) after the \(k\)-th iteration as the midpoint

\[x_k=\frac{a_k+b_k}{2}\]

of \(I_k\). Since the actual solution \(f(c)=0\) satisfies \(c\in I_k\), we have

\[|x_k-c|\leq\frac{1}{2}|I_k|\]

where \(|I_k|\) symbolizes the length of the interval \(I_k\). Since the length of the current search interval gets divided in half in each iteration, we have

\[|e_k|=|x_k-c|\leq \left(\frac{1}{2}\right)^k|I_0|\]

We interpret this behavior as linear convergence; although we cannot strictly guarantee that \(|e_{k+1}|\leq L|e_k|\) (\(L<1\)) at each iteration, this definition can also be iterated to yield

\[|e_k|\leq L^k|e_0|\]

which is qualitatively equivalent to the expression for bisection. Since the order of convergence is linear, we expect to gain a fixed number (or fixed fraction) of significant digits at each iteration; since \(0.5^{10}\approx 0.001\) we can actually say that the bisection method yields about \(3\) additional correct significant digits after every \(10\) iterations.

The bisection procedure is very robust, by virtue of Bolzano’s theorem, and despite having only linear convergence can be used to find an approximation within any desired error tolerance. It is often used to localize a good initial guess which can then be rapidly improved with a fixed point iteration method such as Newton’s method. Note that bisection search is not a fixed point iteration itself!